Real PSA simulation module (`pyAPEP.simsep`)

This module enables ideal PSA simulation using isotherm function and operating conditions.

First, import simsep into Python after installation.

import pyAPEP.simsep as simsep

Then users need to 10-steps to simulate.

Isotherm selection
Column design
Adsorbent information
Gas property information
Mass transfer information
Thermal information
Boundary condition setting
Initial condition setting
Simulation run
Graph

In next section, detailed steps are explained.

Usage

1. Isotherm selection

Here, we use extended Langmuir isotherm as an example.

\[q_{i} = \frac{q_{m,i}b_{i}P_{i}}{1+\sum^{n}_{j=1}b_{j}P_{j}}\]

First, we need to import some libraries.

import numpy as np
import matplotlib.pyplot as plt

Then, define some parameters of the extended Langmuir isotherm.

# Define parameters of extended Langmuir isotherm
qm1 = 1
qm2 = 0.1
b1 = 0.5
b2 = 0.05

dH1 = 10000     # J/mol
dH2 = 15000     # J/mol
R_gas = 8.3145 # J/mol/K
T_ref = 300    # K

The isotherm is defined as follows.

# Define the isotherm
def extLang(P, T):
    P1 = P[0]*np.exp(dH1/R_gas*(1/T-1/T_ref))
    P2 = P[1]*np.exp(dH1/R_gas*(1/T-1/T_ref))
    deno = 1 + b1*P1 + b2*P2
    q1 = qm1*b1*P1 / deno
    q2 = qm2*b2*P2 / deno
    return q1, q2

2. Column design

# Set the design parameter of a column
col_len         = 1      # (m)
cross_sect_area = 0.0314 # (m^2)
num_comp        = 2
node = 41                # The number of nodes

# Column definition
Column1 = simsep.column(col_len, cross_sect_area, num_comp, N_node= node)

3. Adsorbent information

voidfrac = 0.4                                          # Void fraction
rho      = 1100                                         # Solid density (kg/m^2)
Column1.adsorbent_info(extLang, voidfrac, rho_s = rho)  # Adsorbent information
print(Column1)                                          # Check

4. Gas property information

Mmol = [0.032, 0.044]   # Molecular weights of gases (kg/mol)
visc = [0.01, 0.01]     # Viscosities of gases (Pa sec)

Column1.gas_prop_info(Mmol, visc) # Gas property information
print(Column1)                    # Check

5. Mass transfer information

MTC = [0.05, 0.05]      # Mass transfer coefficients
a_surf = 400            # Volumatric specific surface area (m2/m3)

Column1.mass_trans_info(MTC, a_surf) # Mass transfer information
print(Column1)                       # Check

6. Thermal information

dH_ads = [10000,16000]  # Heat of adsorption (J/mol)
Cp_s = 5                # Solid heat capacity (J/kg K)
Cp_g = [10,10]          # Gas heat capacity (J/mol K)
h_heat = 10             # Heat transfer coefficient between solid and gas (J/m^2 K s)

Column1.thermal_info(dH_ads, Cp_s, Cp_g, h_heat) # Mass transfer information
print(Column1)                                   # Check

7. Boundary condition setting

P_inlet  = 9              # Inlet pressure  (bar)
P_outlet = 8.0            # Outlet pressure (bar)
T_feed   = 300            # Feed in temperature (K)
y_feed = [0.5,0.5]        # Feed composition (mol/mol)

Column1.boundaryC_info(P_outlet, P_inlet, T_feed, y_feed) # Boundary condition
print(Column1)                                            # Check

8. Initial condition setting

P_init = 8*np.ones(node)                       # Initial pressure (bar)
y_init = [0.2*np.ones(node), 0.8*np.ones(node)]  # Gas phase mol fraction (mol/mol)
Tg_init = 300*np.ones(node)                    # Initial gas temperature (K)
Ts_init = 300*np.ones(node)                    # Initial solid temperature (K)

P_partial = [P_init*y_init[0], P_init*y_init[1]] # Partial pressure (bar)
q_init = extLang(P_partial, Ts_init)             # Solid phase uptake (mol/kg)

Column1.initialC_info(P_init, Tg_init, Ts_init, y_init, q_init) # Initial condition
print(Column1)                                                  # Check

9. Simulation run

y, z, t = Column1.run_mamoen(2000, n_sec=10, CPUtime_print=True)

10. Graph

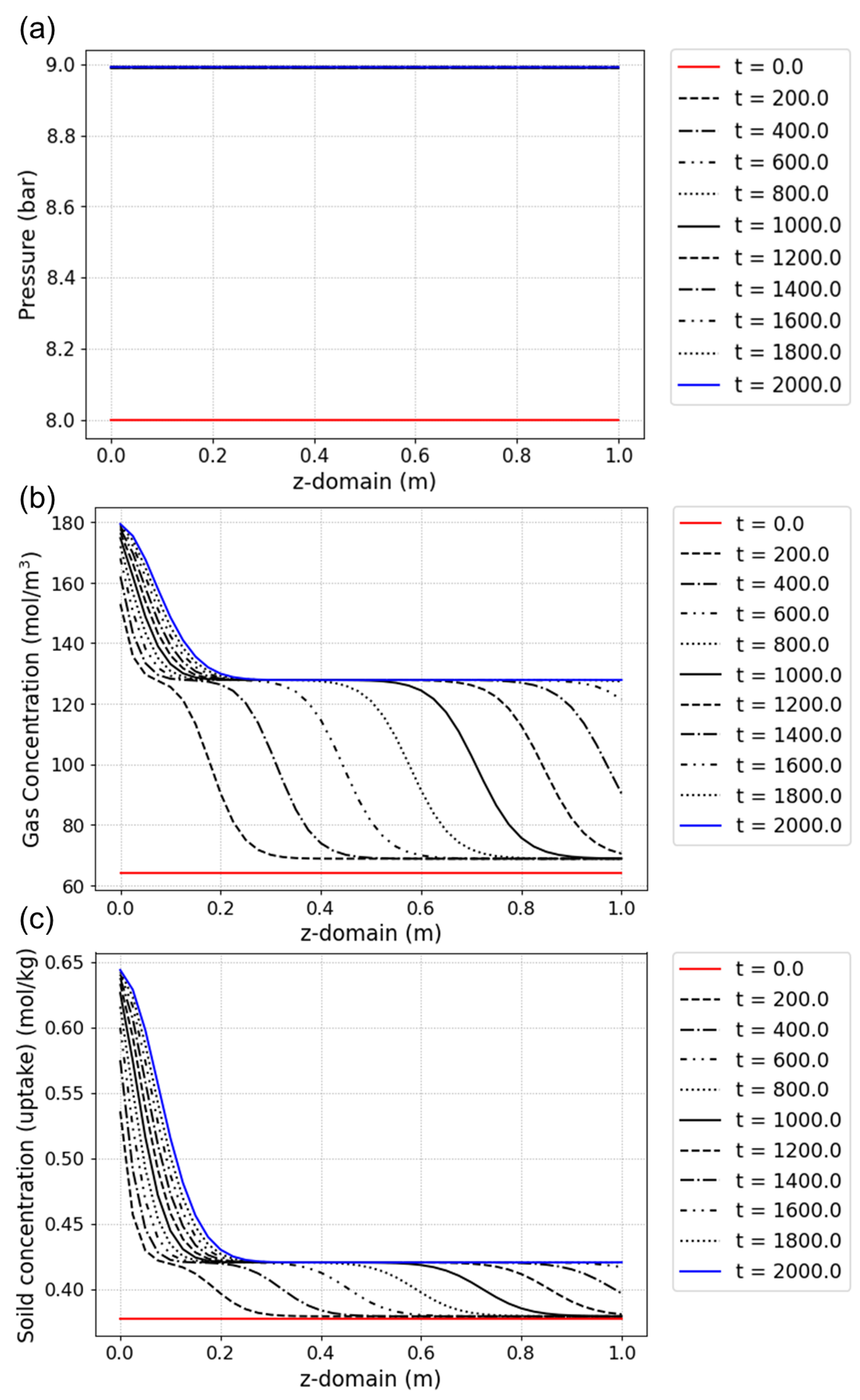
# Simulation result: Pressure according to z-domain
Column1.Graph_P(200,loc = [1.2, 0.9])
# Simulation result: Gas concentration according to z-domain
Column1.Graph(200, 0, yaxis_label=
'Gas Concentration (mol/m$^3$)',loc = [1.2, 0.9])
# Simulation result: Solid concentration according to z-domain
Column1.Graph(200, 2, yaxis_label=
'Soild concentration (uptake) (mol/kg)',loc = [1.2, 0.9])

The results are shown in Fig. (a)–(c)

Class documentation

Real PSA simulation module (`pyAPEP.simsep`)

class pyAPEP.simsep.column(L, A_cross, n_component, N_node=11, E_balance=True)[source]

Instantiation. A Column class is for simulating packed bed column or pressure swing adsroption process.

Parameters:

L – Length of column \((m)\)
A_cross – Cross-sectional area of column \((m^2)\)
n_component – Number of components
N_node – Number of nodes
E_balance – Energy balance inclusion (default = True)

__init__(L, A_cross, n_component, N_node=11, E_balance=True)[source]

__str__()[source]: Return str(self).

adsorbent_info(iso_fn, epsi=0.3, D_particle=0.01, rho_s=1000, P_test_range=[0, 10], T_test_range=[273, 373])[source]

Adsorbent information

Parameters:

iso_fn – Isothem function (Type: n_comp.N array, N array [pressure, temperature])
epsi – Void fraction
D_particle – Particle diameter \((m)\)
rho_s – Solid density \((kg/m^3)\)
P_test_range – Range of pressure for test \((bar)\)
T_test_range – Range of temperature for test \((K)\)

gas_prop_info(Mass_molar, mu_viscosity)[source]

Gas property information

Parameters:

Mass_molar – Molar mass \((mol/kg)\)
mu_viscosity – Viscosity \((Pa \cdot s)\)

mass_trans_info(k_mass_transfer, a_specific_surf, D_dispersion=1e-08)[source]

Mass transfer

Parameters:

k_mass_transfer – mass transfer coefficient \((s^{-1})\)
a_specific_surf – specific surface area \((m^2/m^3)\)
D_dispersion – dispersion coefficient \((m^2/s)\)

thermal_info(dH_adsorption, Cp_solid, Cp_gas, h_heat_transfer, k_conduct=0.0001, h_heat_ambient=0.0, T_ambient=298.15)[source]

Thermal information

Parameters:

dH_adsorption – Heat of adsorption \((J/mol)\)
Cp_solid – Solid heat capacity \((J/kg \cdot K)\)
Cp_gas – Gas heat capacity \((J/mol \cdot K)\)
h_heat_transfer – Heat transfer coefficient between solid and gas \((J/m^2 \cdot K \cdot s)\)
k_conduct – Conductivity of solid phase in axial direction \((W/m \cdot K)\)
h_heat_ambient – Heat transfer coefficient between ambient air and outer surface of the column \((J/m^2 \cdot K \cdot s)\)
T_ambient – Abient temperature \((K)\)

boundaryC_info(P_outlet, P_inlet, T_inlet, y_inlet, Cv_in=0.1, Cv_out=0.001, Q_inlet=None, assigned_v_option=True, foward_flow_direction=True)[source]

Boundary condition information

Parameters:

P_outlet – Outlet pressure \((bar)\) [scalar]
P_inlet – Inlet pressure \((bar)\) [scalar]
T_inlet – Inlet temperature \((K)\) [scalar]
y_inlet – Inlet composition \((mol/mol)\) [n_comp array]
Cv_in – Valve constant of inlet side \((m^3/bar \cdot s)\) [scalar]
Cv_out – Valve constant of outlet side \((mol/bar \cdot s)\) [scalar]
Q_inlet – Volumetric flow rate \((m^3/s)\)
assigned_v_option – Assign velocity or not [Boolean]
foward_flow_direction – Flow direction, if this is ‘True’ then the flow direction is foward.

initialC_info(P_initial, Tg_initial, Ts_initial, y_initial, q_initial)[source]

Initial condition

Parameters:

P_initial – Initial pressure \((bar)\) [N array]
Tg_initial – Initial gas temperature \((K)\) [N array]
Ts_initial – Initial solid temperature \((K)\) [N array]
y_initial – Gas phase mol fraction \((mol/mol)\) [n_comp N array]
q_initial – Solid phase uptake \((mol/kg)\) [n_comp N array]

run_mamo(t_max, n_sec=5, CPUtime_print=False)[source]

Run mass & momentum balance equations

Parameters:

t_max – Maximum time domain value
n_sec – Number of time node per second
CPUtime_print – Print CPU time

run_mamoen_alt(t_max, n_sec=5, CPUtime_print=False)[source]

Run mass & momentum balance alternative

Parameters:

t_max – Maximum time domain value
n_sec – Number of time node per second
CPUtime_print – Print CPU time

run_mamoen(t_max, n_sec=5, CPUtime_print=False)[source]

Run mass & momentum & energy balance

Parameters:

t_max – Maximum time domain value
n_sec – Number of time node per second
CPUtime_print – Print CPU time

next_init(change_init=True)[source]

Next initalization

Parameters:: change_init – Replace inital condition with previous result at final time [boolean]
Returns:: Previous result at final time (if this is ‘True’, initial conditions are repalced automatically)

change_init_node(N_new)[source]

Initial node change

Parameters:: N_new – New number of nodes

Q_valve(draw_graph=False, y=None)[source]

Q valve

Parameters:

draw_graph – Show graph [boolean]
y – Simulation result of run_mamo and run_mamoen (if it is ‘None’, this value is from the simulation result automatically)

Returns:

Volumetric flow rates at Z = 0 and L [time_node array]

breakthrough(draw_graph=False)[source]: Breakthrough

Graph(every_n_sec, index, loc=[1, 1], yaxis_label=None, file_name=None, figsize=[7, 5], dpi=85, y=None)[source]

Making graph

Parameters:

every_n_sec – Number of points in graph
index – Index determining which graph is to be displayed = 0 - n_comp-1 gas concentration \((mol/m^3)\) / n_comp - 2 n_comp - 1 solid phase uptake \((mol/kg)\) / 2 n_comp gas phase temperature \((K)\) / 2 n_comp + 1 solid phase temeprature
loc – Location of legend
yaxis_label – ylabel of graph
file_name – File name
figsize – Figure size (default [7,5])
dpi – Dot per inch (default 85)
y – Gas phase mol fraction \((mol/mol)\) [n_comp N array]

Graph_P(every_n_sec, loc=[1, 1], yaxis_label='Pressure (bar)', file_name=None, figsize=[7, 5], dpi=85, y=None)[source]

Making graph of partial pressure

Parameters:

every_n_sec – Number of points in graph
loc – Location of legend
yaxis_label – ylabel of graph
file_name – File name
figsize – Figure size (default [7,5])
dpi – Dot per inch (default 85)
y – Gas phase mol fraction \((mol/mol)\) [n_comp N array]

copy()[source]: Copy

__weakref__: list of weak references to the object (if defined)

pyAPEP.simsep.step_P_eq_alt1(column1, column2, t_max, n_sec=5, Cv_btw=0.1, valve_select=[1, 1], CPUtime_print=False)[source]

pyAPEP.simsep.step_P_eq_alt2(column1, column2, t_max, n_sec=5, Cv_btw=0.1, valve_select=[1, 1], CPUtime_print=False)[source]

pyAPEP.simsep.step_P_eq(column1, column2, t_max, n_sec=5, Cv_btw=0.1, valve_select=[1, 1], CPUtime_print=False)[source]

Theory

Mass balance

The mass balance relationship, shown below, is used to describe the pressure swing adsorption process.

\[\frac{\partial C_{i}}{\partial t} = -\frac{\partial (uC_{i})}{\partial z} + D_{dis} \frac{\partial^2 C_{i}}{\partial z^2} - \rho_{s}\frac{(1-\epsilon)}{\epsilon}\frac{\partial q_{i}}{\partial z_{i}}\]

where

\(C_{i} =\) Concentration of component i \((mol/m^3)\)

\(t =\) Time \((s)\)

\(D_{dis} =\) Dispersion coefficient \((m^2/s)\)

\(z =\) Length in axial direction \((m)\)

\(\epsilon =\) Void fraction \((m^3/m^3)\)

\(\rho_{s} =\) Density of solid \((kg/m^3)\)

\(q_{i} =\) Uptake of component i \((mol/kg)\)

Momentum balance 

In the adsorption process simulation, the pressure drop \(\Delta P\) should be considered to solve the momentum balance along the length of the bed. In 1952, Ergun proposed an equation to consider \(\Delta P\) in a packed bed, and the same equation was used to solve the momentum balance in this package, similar to many previous studies.

The Ergun equation represents the relationship between the pressure drop and resultant fluid flow in packed beds, as shown below. The equation was derived from experimental measurements and theoretical postulates.

\[- \frac{\partial P}{\partial z} = \frac{180 \mu }{d_{p}^2 } \frac{(1 - \varepsilon)^2}{\varepsilon^3} u + \frac{7}{4} \frac{\rho_{f}}{d_{P}} \frac{1 - \varepsilon}{\varepsilon^3} u|{u}|\]

where

\(\partial P =\) Pressure drop \((bar)\)

\(L =\) Height of the bed \((m)\)

\(\mu =\) Fluid viscosity \((Pa \cdot s)\)

\(\varepsilon =\) Void space of the bed

\(u =\) Fluid superficial velocity \((m/s)\)

\(d_{P} =\) Particle diameter \((m)\)

\(\rho_{f} =\) Density of Fluid \((kg/m^3)\)

Energy balance 

The energy balance, shown below, is also used to describe the pressure swing adsorption process.

\[Convection = -CC_{p,g}u\frac{\partial T_{g}}{\partial z} \frac{h}{\varepsilon}a_{surf}(T_{s}-T_{g})\]

\[Conduction = \lambda_{cond} \frac{\partial^{2} T_{s}}{\partial z^{2}}\]

\[Generation = \sum_{i=1}^{n}(-\Delta H_{ad,i})\rho_{s} (1-\varepsilon) \frac{\partial q_{i}}{\partial t}\]

The overall energy balance under the boundary condition for the gas phase:

\[\sum_{i=1}^{n}C_{i}C_{p,i}\frac{\partial T_{g}}{\partial t} = h a_{surf} (T_{s} - T_{g}) -\sum_{i=1}^{n}uC_{i}C_{p,i}\frac{\partial T_{g}}{\partial z}\]

The overall energy balance under the boundary condition for the solid phase:

\[\begin{split}\left( (1-\varepsilon) \rho_{s} \sum_{i=1}^{n} (q_{i} C_{p,i}) + \rho_{s}C_{p,s} \right) &\frac{\partial T_{s}}{\partial t} = h a_{surf}(T_{g} - T_{s}) + \lambda_{cond} \frac{\partial^{2} T_{s}}{\partial z^{2}}\\ +&\sum_{i=1}^{n}(-\Delta H_{ad,i})\rho_{s} (1-\varepsilon) \frac{\partial q_{i}}{\partial t}\end{split}\]

where

\(C =\) Concentration \((mol/m^3)\)

\(C_{p, g} =\) Gas heat capacity \((J/mol \cdot K)\)

\(T_{g} =\) Gas temperature \((K)\)

\(t =\) Time \((s)\)

\(u =\) Velocity \((m/s)\)

\(z =\) Length in axial direction \((m)\)

\(h =\) Enthalpy \((J/m^2 \cdot K \cdot s)\)

\(\varepsilon =\) Void fraction \((m^3/m^3)\)

\(a_{surf} =\) Interfacial area concentration \((m^2/m^3)\)

\(T_{s} =\) Solid temperature \((K)\)

\(\rho_{s} =\) Density of solid \((kg/m^3)\)

\(q_{i} =\) Uptake of component i \((mol/kg)\)

Real PSA simulation module (pyAPEP.simsep)

Usage

1. Isotherm selection

2. Column design

3. Adsorbent information

4. Gas property information

5. Mass transfer information

6. Thermal information

7. Boundary condition setting

8. Initial condition setting

9. Simulation run

10. Graph

Class documentation

Real PSA simulation module (pyAPEP.simsep)

Theory

Mass balance

Momentum balance

Energy balance

Real PSA simulation module (`pyAPEP.simsep`)

Real PSA simulation module (`pyAPEP.simsep`)

Momentum balance 

Energy balance 